(Edit: This article is a more in-depth writeup of an algorithm that I developed around 2005, and first posted to Martin Baker’s Euclidean Space website. That time was the height of the Intel NetBurst architecture, which was notorious for its deep pipeline and high branch misprediction penalty. Hence the motivation to develop a branch-free matrix to quaternion conversion routine. What follows is the complete derivation and analysis of this idea.)
The original routine to convert a matrix to a quaternion was given by Ken Shoemake [1] and is very branchy. There is a way to eliminate these branches and arrive at a completely branch-free and highly parallelizable code. The trade off is the introduction of 3 additional square roots. Jump to the analysis section and the end of this article, or continue fist with the math bits.
Trade 3 roots for a branch
When a quaternion with elements ![]() is converted to a matrix
is converted to a matrix ![]() , the terms that finally end up in the matrix can be added and subtracted to arrive at a wealth of identities. The elements in the matrix diagonal are related to the quaternion elements by
, the terms that finally end up in the matrix can be added and subtracted to arrive at a wealth of identities. The elements in the matrix diagonal are related to the quaternion elements by
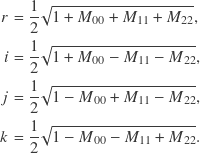
The off-diagonal matrix elements are related to the quaternion elements by
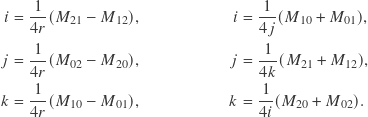
It is obvious that there are multiple paths to restore the quaternion from a matrix. One could first restore ![]() from the diagonal elements, and then use the off-diagonal elements to restore
from the diagonal elements, and then use the off-diagonal elements to restore ![]() ,
, ![]() and
and ![]() . Or first restore
. Or first restore ![]() from the diagonal elements, and then use the off-diagonal for the rest, etc. The standard, branchy conversion code just does that. Can we eliminate the branches and just use the diagonal elements for everything? In theory, yes, the only thing missing would be the signs.
from the diagonal elements, and then use the off-diagonal for the rest, etc. The standard, branchy conversion code just does that. Can we eliminate the branches and just use the diagonal elements for everything? In theory, yes, the only thing missing would be the signs.
void BranchlessMatrixToQuaternion( float out[4], float in[3][3] ) { out[0] = .5 * sqrt( max( 0, 1 + in[0][0] + in[1][1] + in[2][2] ) ); // r out[1] = .5 * sqrt( max( 0, 1 + in[0][0] - in[1][1] - in[2][2] ) ); // i out[2] = .5 * sqrt( max( 0, 1 - in[0][0] + in[1][1] - in[2][2] ) ); // j out[3] = .5 * sqrt( max( 0, 1 - in[0][0] - in[1][1] + in[2][2] ) ); // k out[1] = copysign( out[1], in[2][1] - in[1][2] ); // i out[2] = copysign( out[2], in[0][2] - in[2][0] ); // j out[3] = copysign( out[3], in[1][0] - in[0][1] ); // k } |
Mathematically, if the matrix ![]() has a determinant of one, then
has a determinant of one, then ![]() cannot be negative, and all four square roots are defined. In practice there can be rounding errors, so to be safe the terms are clamped with
cannot be negative, and all four square roots are defined. In practice there can be rounding errors, so to be safe the terms are clamped with max( 0, ... ) before the square roots are taken. The off diagonal elements are only used to restore the missing signs. Since only the signs matter, the division by ![]() can be lifted! (The function
can be lifted! (The function copysign is supposed to transfer the sign bit from one floating point number to another, and your compiler should do a decent job and reduce it to some sequence of bitwise and/or instructions. Clang and GCC do this on x86 with SSE floating point. See the comment section for a discussion about this.)
Compared with the original conversion code, there are four square roots instead of one square root and one division, but there aren’t any branches. The code pipelines well (all the square roots can run in parallel, followed by all the copysigns).
Operation Counts
In the following table of operation counts, I have included a max( 0, ... ) safeguard also in the Shoemake algorithm (the original doesn’t have this). The copysign is regarded as a single operation.
| Shoemake | Branchless | |
|---|---|---|
| add/sub/mul/max | 11..13 | 23 |
| div/sqrt | 2 | 4 |
| floating point compare |
1..3 | 0 |
| branch | 1..3 | 0 |
| copysign | 0 | 3 |
| steps in longest dependency chain |
8..15 | 6 |
Let’s assume the latency of sqrt and div as 15 cycles (single precision), the latency of a branch as 2 cycles with a misprediction penalty of 15 cycles, and the average latency of everything else as 3 cycles. These numbers are in the ballpark of Intel Wolfdale resp. AMD Jaguar processors [2]. Depending on whether the execution is assumed to be either perfectly serial and in-order (a simple addition of all the latencies), or assumed to be perfectly parallel and out-of-order (the sum of the latencies in the longest dependency chain), we get the cycle counts shown in the table below. The reality should be anywhere between these extremes.
| Shoemake | Branchless | |
|---|---|---|
| perfectly serial (in-order) | 68..129 | 138 |
| perfectly parallel (out of order) | 49..88 | 30 |
Numerical Stability
The catch of the branchless algorithm is that the singularity at the rotation angle of 180° is still there. Although the division by ![]() was lifted and so a division by zero cannot occur, it now appears as random signs from catastrophic cancellation. Take for example, a 180° rotation around the x‑y diagonal,
was lifted and so a division by zero cannot occur, it now appears as random signs from catastrophic cancellation. Take for example, a 180° rotation around the x‑y diagonal,
![Rendered by QuickLaTeX.com \[\left( \begin{array}{d{0}d{0}d{0}} 0 & 1 & \epsilon \\ 1 & 0 & -\epsilon \\ -\epsilon & \epsilon & -1 \end{array} \right) .\]](http://www.thetenthplanet.de/wordpress/wp-content/ql-cache/quicklatex.com-6d7dfc611d38041406e5e51ef64905ae_l3.png)
In an ideal world, when the rotation angle travels through a small neighborhood around the point of 180°, the value of ![]() vanishes and changes sign. The
vanishes and changes sign. The ![]() and
and ![]() components of the resulting quaternion should then flip signs simultaneously too. In reality however, with just the tiniest amount of rounding error, these signs are quasi random. The behavior can be described like this:
components of the resulting quaternion should then flip signs simultaneously too. In reality however, with just the tiniest amount of rounding error, these signs are quasi random. The behavior can be described like this:
| just before 180° (consistent signs) |
at 180° (random signs) |
just after 180° (consistent signs) |
|---|---|---|
Recommendation
A configuration which provokes the singularity described above is surprisingly common as an exchange of coordinate axes (conversion from Z‑up to Y‑up, for example). Where the branchless algorithm shines however is the conversion of local animation keys. These rarely cross a 180° rotation angle. In one use case for me, the skeleton is the skeleton of a plant and the animation is driven by physics, and I know or can make sure that a rotation of 180° simply doesn’t occur.
Given this knowledge, the branchless conversion code is recommended over the standard one, under the condition that the rotation angle does not cross 180°.
References
[1] Ken Shoemake, “Quaternions”,
http://www.cs.ucr.edu/~vbz/resources/quatut.pdf
[2] Instruction Tables at Agner Optimization
http://www.agner.org/optimize/instruction_tables.pdf
On PPC architectures, I would recommend *not* doing copysign() with bit operations, because that incurs a LHS penalty. On those architectures, you are better of implementing copysign() using fabs() and a floating-point select.
Like the branchless version, will come in handy in the future!
While I was thinking in the lines of ORPS and ANDPS when I wrote the mention of bit-operations, you’re right, this load-hit-store thing is nasty, and using fsel is a good idea, however it seems the GCC people at least have already taken care of that http://www.archivum.info/gcc-patches@gcc.gnu.org/2005–01/00805/(PATCH)-fast-Copysign-for-PPC–flag_unsafe_math_optimizations-only.html
Dear Christian,
It seems your code may avoid several additions/subtractions.
See below f90 implementation.
Alex
===========================================
Hi Alex,
Yes, the code that I showed in the article does not aggressively combine common subexpressions, as your code does. I did this for clarity and under the assumption that the compiler could do something similar, if given the liberty to do so (eg. ‑ffast-math and co). In any case, thanks for your contribution!
EDIT: On a side note, factoring out common sub expressions increases the length of the dependency chain, so it would be arguable if that is really faster with out-of-order execution. In any case, measurement over opinion!