White Light equals Brown Noise

Here is a recent shower thought:

It is usually said that the colors of noise are inspired by the spectral distributions of corresponding colors of light. For example, the ‘white’ in white noise is an allusion to white light which is thought to have a (mostly) flat spectrum. But is this so? How does white light actually look like, as an electromagnetic wave?

So I made following figure which shows some power-law distributions in the visible range of wavelengths colored by their theoretical appearance:

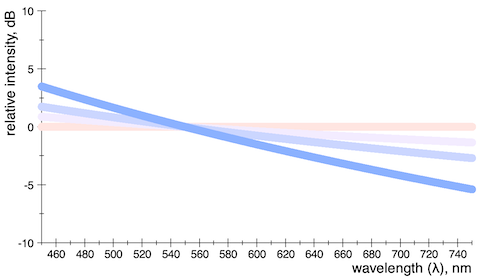
Fig 1: Spectral distributions with exponents from 0 to −4.

The color of the flat line is also known as Standard Illuminant E‍‍ – or equal-energy white light. Compared to the D65 white background it has a rather pinkish appearance with a correlated color temperature of about 5500 K.

The other extreme is a distribution where the spectral intensity is inversely proportional to the wavelength raised to the fourth power, or $\mathrm{d}I \sim \lambda^{-4} \mathrm{d}\lambda$ ‍. This was both the color of pure Rayleigh scattering (sky blue) and also thermal radiation in the limit of infinite temperature.

Now wait a minute. White noise is defined as a flat frequency spectrum, but white light is defined as a flat wavelength spectrum. This is generally not the same: To convert a “per wavelength” distribution to a “per frequency” distribution one must do a proper change of variable.

So let’s convert the distributions from above from wavelength $\lambda$ to wavenumber $\nu$ (that’s the greek letter ν). In doing so, the distribution acquires an additional factor of $1 \over \nu^2$ ‍, since $\lambda$ and $\nu$ are reciprocals of one another:

$\int I_\lambda(\lambda) \mathrm{d}\lambda \Leftrightarrow \int I_\nu(\nu) {\mathrm{d}\lambda \over \mathrm{d}\nu} \operatorname{d}\nu \Leftrightarrow \int {I_\nu(\nu) \over \nu^2} \mathrm{d}\nu .$

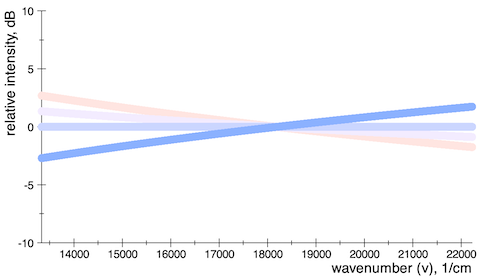
Fig 2: The same distributions as in fig. 1, but now as a wavenumber spectrum. The customary unit for wavenumber is cm^-1.

So who is the flat one now?

It turns out that the middle guy, the distribution that follows an exponent of −2 in the wavelength picture (color temperature about 10000 K) is the flat one in the wavenumber picture. An electromagnetic wave in the shape of white noise – in the visual band at least – should therefore appear as this color.

On the other hand, what is usually called white light now follows an exponent of −2 in the wavenumber picture (–6 dB per octave). White light equals brown noise! In fact, for any power-law distribution we have

$\int \lambda^{-\alpha} \mathrm{d}\lambda \Leftrightarrow \int \nu^{\alpha-2} \mathrm{d}\nu ,$

which leads to the fact that the distribution with an exponent of −1 is the same in both pictures. This is the pale colored one with a color temperature of about 7000 K.

So to summarize, the white in “white noise” is, in fact, a blatant misunderstanding :)

power laws		noise	color
$I_\lambda \operatorname{const.}$	$I_\nu \sim \nu^{-2}$	brown	5456 K	Illuminant E
$I_\lambda \sim \lambda^{-1}$	$I_\nu \sim \nu^{-1}$	pink	7029 K	invariant exponent
$I_\lambda \sim \lambda^{-2}$	$I_\nu \operatorname{const.}$	white	9926 K	EM white noise
$I_\lambda \sim \lambda^{-4}$	$I_\nu \sim \nu^{2}$	blue	∞ K	Sky blue

The Tenth Planet

If it existed

White Light equals Brown Noise

Schreibe einen Kommentar Antworten abbrechen

Please answer the following anti-spam test